Один Дюйм Равен См

Ответом к заданиям 1—12 является целое число или конечная десятичная дробь. Дробную часть от целой отделяйте десятичной запятой. Единицы измерений писать не нужно.

Если ва­ри­ант задан учителем, вы можете вписать ответы на задания части С или загрузить их в систему в одном из графических форматов. Учитель уви­дит ре­зуль­та­ты вы­пол­не­ния заданий части В и смо­жет оце­нить за­гру­жен­ные от­ве­ты к части С. Вы­став­лен­ные учи­те­лем баллы отоб­ра­зят­ся в вашей статистике.

Рост че­ло­ве­ка 6 футов 1 дюйм. Вы­ра­зи­те его рост в сан­ти­мет­рах, если 1 фут равен 12 дюй­мам. Счи­тай­те, что 1 дюйм равен 2, 54 см. Ре­зуль­тат округ­ли­те до це­ло­го числа сан­ти­мет­ров.

Ответ:

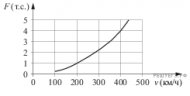
Когда са­мо­лет на­хо­дит­ся в го­ри­зон­таль­ном по­ле­те, подъ­ем­ная сила, дей­ству­ю­щая на кры­лья, за­ви­сит толь­ко от ско­ро­сти. На ри­сун­ке изоб­ра­же­на эта за­ви­си­мость для не­ко­то­ро­го са­мо­ле­та. На оси абс­цисс от­кла­ды­ва­ет­ся ско­рость (в ки­ло­мет­рах в час), на оси ор­ди­нат – сила (в тон­нах силы). В не­ко­то­рый мо­мент подъ­ем­ная сила рав­ня­лась одной тонне силы. Опре­де­ли­те по ри­сун­ку, на сколь­ко ки­ло­мет­ров в час надо уве­ли­чить ско­рость, чтобы подъ­ем­ная сила уве­ли­чи­лась до 4 тонн силы?

Ответ:

Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

Ответ:

На кон­фе­рен­цию при­е­ха­ли 6 уче­ных из Ита­лии, 3 из Гер­ма­нии и 3 из Рос­сии. Каж­дый из них де­ла­ет на кон­фе­рен­ции один до­клад. По­ря­док до­кла­дов опре­де­ля­ет­ся же­ребьёвкой. Най­ди­те ве­ро­ят­ность того, что тре­тьим ока­жет­ся до­клад уче­но­го из Гер­ма­нии.

Ответ:
Ответ:

Угол при вер­ши­не, про­ти­во­ле­жа­щей ос­но­ва­нию рав­но­бед­рен­но­го тре­уголь­ни­ка, равен 150°. Бо­ко­вая сто­ро­на тре­уголь­ни­ка равна 21. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

Ответ:

На ри­сун­ке изоб­ражён гра­фик функ­ции = () и семь точек на оси абс­цисс: 1, 2, 3..., 7. В сколь­ких из этих точек про­из­вод­ная функ­ции по­ло­жи­тель­на?

Ответ:

Най­ди­те пло­щадь по­верх­но­сти мно­го­гран­ни­ка, изоб­ражённого на ри­сун­ке (все дву­гран­ные углы пря­мые).

Ответ:

Най­ди­те , если .

Ответ:

10

Для обо­гре­ва по­ме­ще­ния, тем­пе­ра­ту­ра в ко­то­ром под­дер­жи­ва­ет­ся на уров­не , через ра­ди­а­тор отоп­ле­ния про­пус­ка­ют го­ря­чую воду. Рас­ход про­хо­дя­щей через трубу ра­ди­а­то­ра воды m = 0, 6 кг/с. Про­хо­дя по трубе рас­сто­я­ние x, вода охла­жда­ет­ся от на­чаль­ной тем­пе­ра­ту­ры до тем­пе­ра­ту­ры T, причём , где — теплоёмкость воды, — ко­эф­фи­ци­ент теп­ло­об­ме­на, а — по­сто­ян­ная. Най­ди­те, до какой тем­пе­ра­ту­ры (в гра­ду­сах Цель­сия) охла­дит­ся вода, если длина трубы ра­ди­а­то­ра равна 144 м.

Ответ:

11

Каж­дый из двух ра­бо­чих оди­на­ко­вой ква­ли­фи­ка­ции может вы­пол­нить заказ за 16 часов. Через 2 часа после того, как один из них при­сту­пил к вы­пол­не­нию за­ка­за, к нему при­со­еди­нил­ся вто­рой ра­бо­чий, и ра­бо­ту над за­ка­зом они до­ве­ли до конца уже вме­сте. Сколь­ко часов по­тре­бо­ва­лось на вы­пол­не­ние всего за­ка­за?

Ответ:

12

Най­ди­те наи­мень­шее зна­че­ние функ­ции на от­рез­ке .

Ответ:

13

Решения заданий части С не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

14

На ребре AA1 пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да ABCDA1111 взята точка так, что 1 : EA = 1 : 2, на ребре BB1 — точка так, что 1 : FB = 1 : 5, а точка — се­ре­ди­на ребра 11. Из­вест­но, что AB = 4, AD = 2, AA1 = 6.

а) До­ка­жи­те, что плос­кость EFT про­хо­дит через вер­ши­ну 1.

б) Най­ди­те угол между плос­ко­стью EFT и плос­ко­стью BB11.

Решения заданий части С не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

15

Решения заданий части С не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

16

17

В ян­ва­ре 2000 года став­ка по де­по­зи­там в банке «Воз­рож­де­ние» со­ста­ви­ла % го­до­вых, тогда как в ян­ва­ре 2001 года — % го­до­вых, при­чем из­вест­но, что + = 30%. В ян­ва­ре 2000 года вклад­чик от­крыл счет в банке «Воз­рож­де­ние», по­ло­жив на него не­ко­то­рую сумму. В ян­ва­ре 2001 года, по про­ше­ствии года с того мо­мен­та, вклад­чик снял со счета пятую часть этой суммы. Ука­жи­те зна­че­ние при ко­то­ром сумма на счету вклад­чи­ка в ян­ва­ре 2002 года ста­нет мак­си­маль­но воз­мож­ной.

Решения заданий части С не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

18

Найти все зна­че­ния па­ра­мет­ра при каж­дом из ко­то­рых среди зна­че­ний функ­ции есть ровно одно целое число.

Решения заданий части С не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

19

В игре «Дро­ти­ки» есть 20 на­руж­ных сек­то­ров, про­ну­ме­ро­ван­ных от 1 до 20 и два цен­траль­ных сек­то­ра. При по­па­да­нии в на­руж­ный сек­тор игрок по­лу­ча­ет ко­ли­че­ство очков, сов­па­да­ю­щее с но­ме­ром сек­то­ра, а за по­па­да­ние в цен­траль­ные сек­то­ра он по­лу­ча­ет 25 или 50 очков со­от­вет­ствен­но. В каж­дом из на­руж­ных сек­то­ров есть об­ла­сти удво­е­ния и утро­е­ния, ко­то­рые, со­от­вет­ствен­но, удва­и­ва­ют или утра­и­ва­ют но­ми­нал сек­то­ра. Так, на­при­мер, по­па­да­ние в сек­тор 10 (не в зоны удво­е­ния и утро­е­ния) дает 10 очков, в зону удво­е­ния сек­то­ра ― 20 очков, в зону утро­е­ния ― 30 очков.

а) Может ли игрок тремя брос­ка­ми на­брать ровно 167 очков?

б) Может ли игрок ше­стью брос­ка­ми на­брать ровно 356 очков?

в) С по­мо­щью ка­ко­го наи­мень­ше­го ко­ли­че­ства брос­ков, игрок может на­брать ровно 1001 очко?

Решения заданий части С не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно. Времени прошло: 0:00:00 Времени осталось: 3:55:00

Завершить тестирование, свериться с ответами, увидеть решения; если работа задана учителем, она будет ему отправлена.